全包圆数学中的完美形状
全包圆的定义与特点

全包圆,又称为完全多边形或轮廓图,是指在平面内,任意多个凸多边形的外接圆,其所有顶角之和等于360度。全包圆不仅是几何学中一个基本概念,也是计算机图形学、信息可视化等领域中的重要工具。它能够帮助我们更好地理解和分析复杂图形的结构。
全包圆在设计中的应用

在设计领域,全包圆被广泛用于布局优化和空间分配。例如,在排版设计中,全包圆可以帮助我们找到最紧凑且美观的文字排列方式。在产品设计中,全包圆有助于创造出既实用又美观的产品外观。当我们的产品需要包含许多不同大小和形状的组件时,全包圔回避了这些组件之间可能出现的问题,如重叠或空隙,从而确保整体设计更加合理、高效。
全 包 圆 在 计 算 机 图 形 学 中 的 应 用
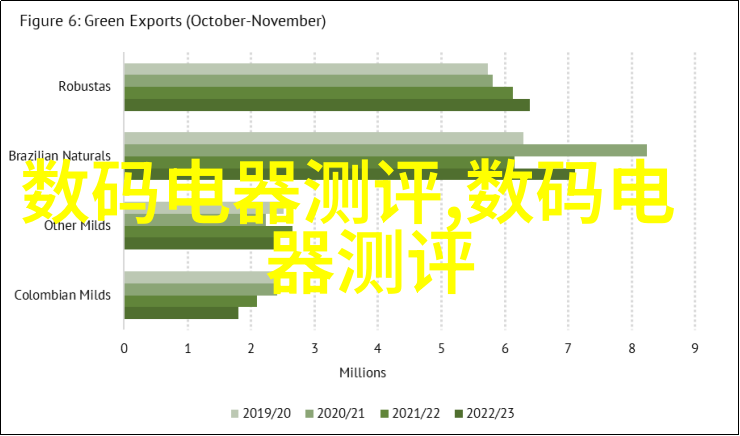
计算机图形学中,全包球是一种常用的数据可视化技术,它通过将三维数据投影到二维平面上来表示,这样就可以有效地展示大量数据并进行分析。此外,全 包 圆 还 被 用 来 实现 交 叉 切 面 可 视 化,例如当我们想要了解两个不同的数据集如何相互作用时,可以使用全 包 圆 来显示交叉切片,从而揭示隐藏关系。
全 包 圆 在 数 学 教 学 中 的 作 用

数学教育中,学习全 包 圆 对学生来说是一个挑战,但也是一个成长机会。通过研究全 包 圆,我们可以提高对几何知识理解深度,对线性代数、拓扑学等高级数学概念有更直观的认识。这对于培养学生解决实际问题能力至关重要,因为无论是在科学研究还是工程实践中,都会遇到需要解释空间关系、寻找最佳配置方案的情况。
未来的发展趋势与展望

随着科技不断进步,全 包 圆 也正迎来新的发展浪潮。未来,随着人工智能技术的提升,我们预计会看到更多基于神经网络算法实现自动化处理复杂几何问题的一般方法。而且,与传统手工绘制相比,现在利用软件工具快速生成精确模型变得越来越容易,这也为艺术家、建筑师以及其他专业人员提供了前所未有的灵活性和可能性。



